Si recuerdan, y no se nos han perdido por el camino, en la entrada de ayer nos quedamos con el cálculo de SA+3[A+3] (es decir, elemento A+3 del array S en la iteración A+3) mediante el algoritmo PRGA. No obstante, como les decíamos, no parece muy factible asumir que los valores de S[0], S[1] y S[A+3] permanecerán quietos tras el barajado de KSA. Y aquí es donde entra en juego la estadística; FMS calcularon mediante la fórmula
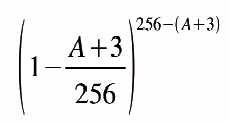
que un 5% de las veces dichos valores no se veían alterados, mientras que el 95% restante no permanecían en las posiciones deseadas. Esto aunque no lo parezca es un dato muy alentador en cuanto a la ruptura del algoritmo se refiere, ya que con una cantidad muy grande de paquetes (del orden de 2000000) se puede detectar que el valor que devuelve el PRGA es nuestro SA+3[A+3].
En este punto recordemos una de las dos premisas que presentamos al comienzo del análisis: conocemos el texto plano del primer byte del paquete, ya que corresponde con el valor 0xAA. Realizando un XOR de ese byte con el primer byte encriptado podemos conocer un 5% de las veces el valor de SA+3[A+3]. Retrocediendo aun mas con este valor podemos calcular el jA+3 y con ello determinar el valor de Clave[A+3]. Una vez determinado el byte A, podremos ir incrementando el valor del índice (A+1) para buscar el siguiente byte de la clave [A+3+1, 255, X], y vuelta a empezar. Poco a poco incrementaremos el valor de A averiguando por completo el total del vector Clave[].
Existen posteriores mejoras del algoritmo FMS que identifican un mayor numero de IVs débiles y que producen como resultado una determinación de la clave con un menor número de paquetes. Personas como KoReK introdujeron nuevas capacidades al algoritmo permitiendo la recuperación de una clave de 128 bits con 800000 IVs y de una de 65 bits con 200000 IVs.
Se ha seguido trabajando en la mejora de este algoritmo, y la universidad de Darmstadt (véase este enlace) ha conseguido rebajar el número de paquetes considerablemente mediante la creación de la herramienta PTW. Haciendo uso de su aplicación es posible conseguir la clave de cifrado (128 bits) con tan solo 50000 IVs. Y con este, queda finalizada la serie de tres “capítulos” sobre porqué no es nada recomendable utilizar WEP (teniendo en cuenta además que WPA suele estar disponible en la mayoría de dispositivos) y porqué su mala fama sí es justificada; pueden obtener más información de este completo artículo de Linux Magazine [PDF] y de innumerables sitios en Internet.
