TIPOS DE CLAVE DE PRODUCTO
A la hora de comprobar la legitimidad de la compra de un software, uno de los métodos más extendidos es la del uso de una clave de compra que se entrega al usuario cuando se compra el acceso al servicio o software. Estas claves deben ser comprobadas en algún punto de la ejecución y utilizar técnicas de ofuscación para que la generación de “keygens” no sea trivial.
Sin embargo, ¿cómo se comprueban estas claves? Aquí podemos encontrarnos con algunas de las siguientes situaciones:
- Uno de los sistemas de seguridad menos seguro es que el binario contuviese una clave o una lista de claves válidas y cuando el usuario introduce su clave, lo único que el programa haga sea comprobar que la clave introducida se encuentra en dicha lista. Esto no aportaría apenas seguridad, ya que un simple análisis de los strings del programa podría recuperar esta clave si no se encuentran correctamente cifradas.
- Otra posibilidad es que nos encontremos con que la clave se compruebe en un servidor remoto, por lo que no tendríamos acceso al binario que realmente la comprueba. En este caso, aunque podamos montar un fake verificator server que simule la respuesta válida del supuesto servidor, no nos serviría en este caso ya que lo que buscamos es obtener claves válidas y consistentes con la aplicación.
- También nos podemos encontrar con la de que la clave se compruebe en el propio binario, pero no directamente comparándolo con una lista de claves “hardcodeadas”, sino comprobando una serie de propiedades de la misma. En este post vamos a centrarnos en éste caso.
Las ventajas de utilizar este tipo de comprobación de claves son varias. En primer lugar, se puede modificar el número de licencias diferentes haciendo el algoritmo más o menos estricto en vez de añadiendo más entradas al pool de claves válidas.
Por otro lado, hay contextos dónde un software no tiene acceso a Internet, por lo que no se puede llevar a cabo la comprobación remota. En este caso, una comprobación por características de la clave tiene más sentido que una lista de claves válidas directamente en el binario, lo cual haría mucho más simple un reversing para extraer las claves.
Aparte, la comprobación de características de la clave, no tiene por qué existir de forma única. Para añadir más seguridad, el software puede llevar varios pasos de verificación, siendo éste el primero antes de, por ejemplo, comprobar la clave remotamente en un segundo paso de verificación.
ROMPIENDO VERIFICACIONES DE CLAVE CON THEOREM PROVERS
Cuando nos encontramos con este tipo de verificaciones en el proceso de análisis de un binario, conocer herramientas para generar rápidamente claves válidas nos puede adelantar mucho el trabajo.
En este caso presentamos Z3 -más conocido por su nombre en inglés, theorem prover-, un demostrador de teoremas de alto rendimiento desarrollado por Microsoft.
Esta herramienta está muy extendida como analizador de satisfacibilidad sobre formulas lógicas. Z3 es un lenguaje de resolución de CSPs (Constraint Satisfaction Problems) o, en castellano, problemas de satisfacción de restricciones, lo que quiere decir que nosotros definiremos propiedades que se deben cumplir (por ejemplo, un entero menor que 2 y mayor o igual a 1), y será el motor de Z3 el que encontrará la solución usando lógica de primer nivel, lo que lo hace una herramienta muy efectiva.
Estos tipos de problemas se resuelven mediante la programación con restricciones, dónde las relaciones entre variables se expresan mediante restricciones en forma de ecuaciones. Una vez se definen estas relaciones (constraints), se utiliza el theorem prover para comprobar que existen soluciones alcanzables, y en caso afirmativo, encontrarlas.
Vamos a ver algunos ejemplos para entender cuál es el potencial de Z3 cómo theorem prover. Para utilizar z3py (librería de Z3 para python), necesitaremos tener instalado python y seguir los pasos que se mencionan en el repositorio de Z3 oficial para compilarlo para nuestro sistema:
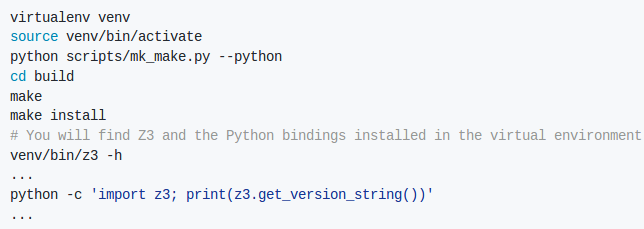

Una vez instalado, y para demostrar el funcionamiento a grandes rasgos de Z3, vamos a realizar un simple algoritmo de validación de claves, el cual simplemente valida que la clave introducida es palíndroma y que tan sólo contiene letras en minúscula:
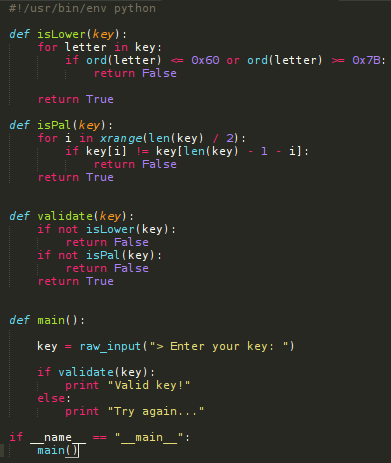
Como vemos, el programa recibe la clave cómo entrada utilizando raw_input(), y realiza 2 comprobaciones. Primero revisa que todos los caracteres ASCII sen encuentren entre 0x60 y 0x7B, es decir, que sean caracteres entre la “a” y la “z” (ambas incluidas) minúsculas. Una vez comprobado, revisa que la palabra sea palíndroma (es decir, que se lee igualmente hacia delante que hacia detrás, por ejemplo, ana).
Hagamos algunas comprobaciones de que funciona:
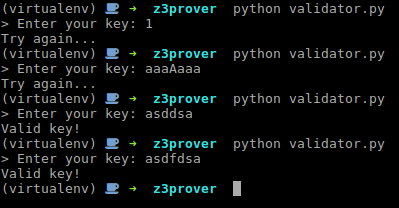
Vemos que efectivamente, las claves que contienen caracteres numéricos o en mayúsculas no son válidos, mientras que una palabra palíndroma cómo “asdfdsa”, sí nos daría acceso.
Una vez que conocemos las características del algoritmo que comprueba la clave, generar el keygen es casi trivial a falta de conocer la sintaxis del theorem prover.

Para ir definiendo la estructura de nuestra solución, en primer lugar vamos a definir las variables de entrada cómo un array de enteros (representando valores ASCII) para que sea más fácil de manipular, el cual declararíamos en la línea 11 con el nombre de las variables que contiene (‘x’ en este caso), y la longitud del array que pasaremos cómo argumento a la función (variable “L” minúscula).
Una vez definido el array e instanciado el Solver (línea 10), vamos añadiendo a este último las constraints que necesitemos. En este caso, recorremos todos los elementos del array, definiendo que el ítem de la posición x, será igual al de la posición x empezando por la cola, aparte de que todos los valores deben estar entre los valores hexadecimales 0x60 y 0x7B (alfabeto de minúsculas).
Una vez añadidas todas las constraints, con el método check podemos obtener si se ha encontrado una solución a la fórmula que satisfaga la misma. Es este caso, s.check() devolverá un objeto “sat” (de satisfaced), y con s.model() podremos obtener la solución.
El resto del algoritmo escrito sirve para encontrar no sólo la primera solución, sino todas las posibles. Para ello, cuando encontramos una solución, la añadimos a la lista de restricciones para que no vuelva a aparecer (línea 31 a 35), y volvemos a llamar al método check (línea 20) para comprobar si sigue existiendo una solución que satisfaga la ecuación.
Veamos un ejemplo de ejecución buscando todas las soluciones entre 30 y 40 caracteres de longitud:
Ahora este ejemplo puede resultar fácil tanto por el hecho de tener el código fuente que valida la clave, cómo por el algoritmo que comprueba la comprueba (un simple ataque de fuerza bruta obtendría soluciones rápidamente), sin embargo no dista mucho de analizar el ensamblador de un binario, comprobar la función que comprueba la clave, y generar un keygen de claves.
Veamos un ejemplo:
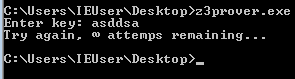
En este caso, tenemos un PE32 que al ejecutar nos muestra el siguiente prompt, simulando una clave de instalación de un software, un CTF de keygen, o cualquier otra cosa que requiera de una credencial para acceder:
Analizando el binario con IDA, llegamos a la función que comprueba la clave introducida:
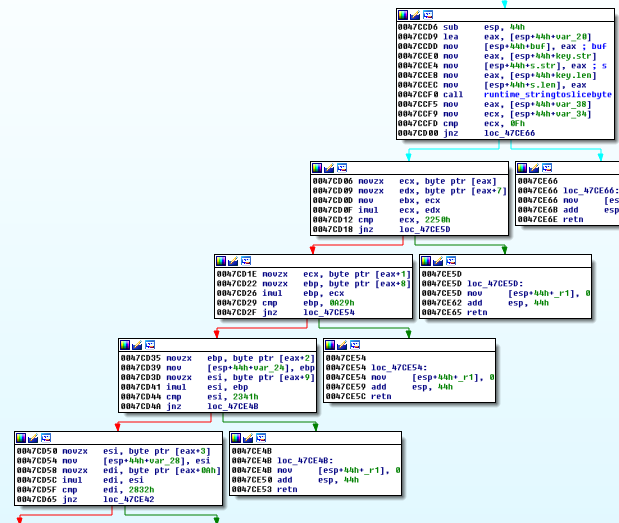
Podemos observar que en la dirección 0x0047CCFD se comprueba que el tamaño de la clave sea de 15 bytes (0Fh), en cuyo caso entrará en una lista de comprobaciones en cascada, que en caso de que las igualdades no se cumplan, se devolverá el valor 0 (false) cómo valor retorno, posiblemente para lanzar el mensaje de clave inválida.
Si cogemos una de estas comprobaciones y lo pasamos a ecuación matemática, podremos traducir las comprobaciones de la siguiente manera:

Si recorremos todas estas comprobaciones, llegaremos a un punto donde tengamos todas las ecuaciones que el binario comprueba sobre la clave, que seguidamente se podrán representar en forma de constraints para Z3 especificando la longitud 15 del array de la siguiente manera:

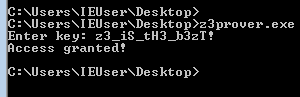
Si ejecutamos Z3 para encontrar todas las soluciones posibles sobre estas costraints, daremos con la única solución válida:

En menos de 1 segundo, Z3 encuentra la solución, que si comprobamos contra el binario, nos dará acceso:
RESUMEN
Gracias a Z3 y a un simple análisis estático hemos encontrado la única clave válida para este binario en cuestión de décimas de segundo, cuando un ataque por fuerza bruta habría tenido un coste temporal mucho superior.
Si el binario tuviese algún tipo de contador de intentos, dónde no sea pensable un ataque por fuerza bruta, esta técnica sería una posible solución para acercarnos a la solución del problema.
Aunque esta herramienta ya lleva tiempo en desarrollo, es ahora cuando se le está empezando a dar utilidad fuera de la comprobación de teoremas, sobre todo en CTFs.
Podemos ver casos dónde Z3 es utilizado en conferencias cómo la DEFCON 2015, dónde la clave de uno de los CTFs era literalmente ‘z3 always helps’, o aplicaciones ingeniosas de la herramienta en otros CTFs cómo el RHme2, del cual nació la idea de este post.
Referencias:
Todo el código generado se encuentra en el siguiente repositorio:
https://github.com/SecurityArtWork/z3prover

